最长回文子串
约 623 个字 38 行代码 1 张图片 预计阅读时间 3 分钟
题目链接: 5. 最长回文子串
中心扩散法
从每一个位置出发,向两边扩散即可。遇到不是回文的时候结束。举个例子,str=acdbbdaa 我们需要寻找从第一个 b(位置为 3)出发最长回文串为多少。怎么寻找?
- 首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
- 然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
- 最后左右双向扩散,直到左和右不相等。如下图所示:
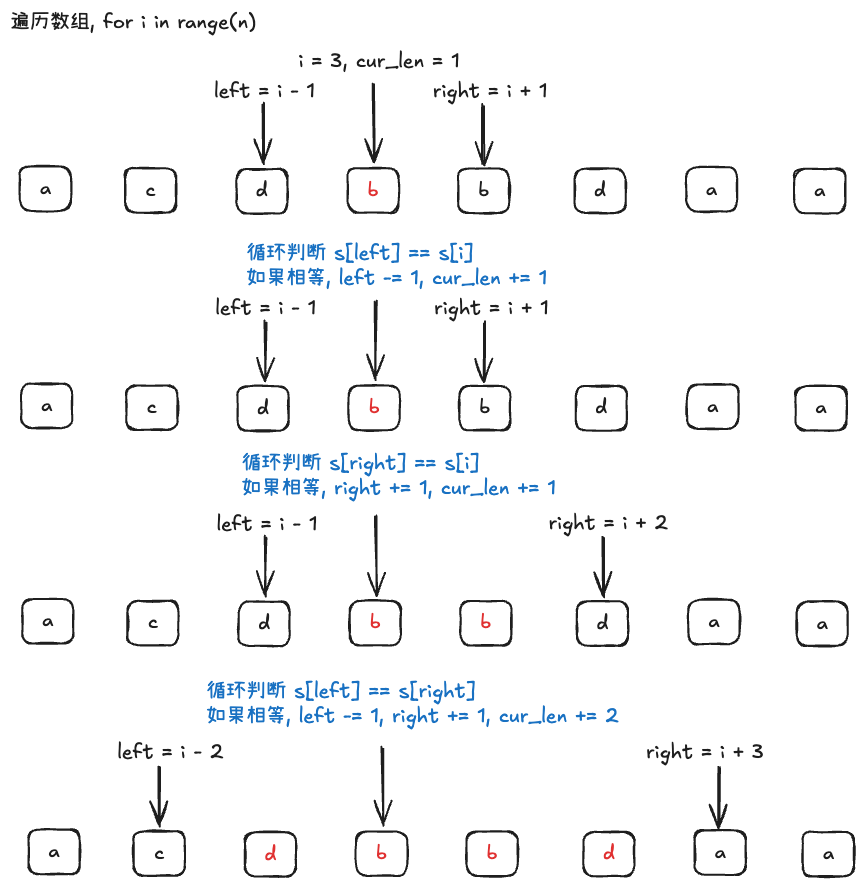
每个位置向两边扩散都会出现一个窗口大小(cur_len)。如果 cur_len > length(用来表示最长回文串的长度)。则更新 length 的值。
因为我们最后要返回的是具体子串,而不是长度,因此,还需要记录一下 length 时的起始位置(start),即此时还要 start = left。
动态规划
中心扩散的方法,其实做了很多重复计算。动态规划就是为了减少重复计算的问题。动态规划听起来很高大上。其实说白了就是空间换时间,将计算结果暂存起来,避免重复计算。作用和工程中用 redis 做缓存有异曲同工之妙。
我们用一个 boolean dp[l][r] 表示字符串从 i 到 j 这段是否为回文。
试想如果 dp[l][r]=true,我们要判断 dp[l-1][r+1] 是否为回文,只需要判断字符串在 (l-1) 和(r+1) 两个位置是否为相同的字符。
进入正题,动态规划关键是找到初始状态和状态转移方程。
初始状态,l=r 时,此时 dp[l][r]=true。
状态转移方程,dp[l][r]=true 并且 (l-1) 和(r+1) 两个位置为相同的字符,此时 dp[l-1][r+1]=true。
if s[l] == s[r] and (r - l <= 2 or dp[l + 1][r - 1]): 这个判断条件的含义是
1. s.charAt(l) == s.charAt(r)
这一部分表示:当前字符串左右两端的字符是否相等。
-
如果 s[l] 和 s[r] 不相等,那么从 l 到 r 之间的子串显然不可能是回文串,因此直接跳过后续判断。
-
如果相等,就进一步判断该子串中间部分是否是回文,从而确定整个子串是否是回文串。
2. (r - l <= 2 || dp[l + 1][r - 1])
这一部分表示:在两种情况下,从位置 l 到 r 的子串可以被确认是回文串。
(1) r - l <= 2
如果 r - l <= 2,说明 l 和 r 之间最多只有 0 个或 1 个字符,这种情况下:
-
s[l] == s[r] 就足以判断该子串是回文串了,因为中间的部分要么为空(r - l = 1),要么只有一个字符(r - l = 2)。
-
示例:对于 aba、aa,只需要两端相等即可确认它们是回文。
(2) dp[l + 1][r - 1]
如果 r - l > 2,说明 l 和 r 之间至少隔着两个字符,那么子串 [l+1, r-1] 是否是回文就变得重要。
-
dp[l + 1][r - 1] 是一个动态规划数组,记录从位置 l+1 到 r-1 的子串是否是回文。
-
如果 dp[l + 1][r - 1] == true,说明该子串是回文串,再加上 s[l] == s[r],可以确认 [l, r] 也是回文串。
-
如果 dp[l + 1][r - 1] == false,那么中间部分不是回文,即使两端字符相等,也无法形成回文串。